Hyperparameter tuning and model stacking using tidymodels in R
In this post you'll learn how to tune the hyperparameters of your models using a variety of tuning grids, how to speed up the search using racing methods and find the optimal set of parameters using simulated annealing. At the end we'll see how we can stack all of our models into a super learner to try and increase performance even more.

Recap from the previous post
Welcome to the second post on the tidymodels packages in R. In the previous post we learnt how to split and pre-process our data and build and measure different regression and classification models. Today's post builds on these learnings and focuses on how we can try and improve our model performance even more by tuning hyperparameters and stacking or ensembling different models to form super learners.
If you've come from the previous post and have all the objects created already that's great. If not, you can run the code below to create everything you need. Before we begin it's worth mentioning that the chapter on grid search in the tidymodels book is definitely worth a read and covers a lot of what we'll be going through today.
The above code sets up the Train and Test data and creates our resampling scheme (10 folds repeated 5 times).
Creating tunable model specifications
To tune hyperparameters in tidymodels we first need to adapt our model specifications. Whereas previously we were creating them with default options, now we can specify the individual hyperparameters we want to tune and tell tidymodels to do this by calling the tune() function. This acts as a placeholder in our specification and tells tidymodels that there is a hyperparameter that will need tuning later on:
Using tune() leaves which values of hyperparameters we want to try up to tidymodels. If we want to use our own values we can simply replace tune() with our chosen vector of values. We can even mix and match a combination of manual values and tune() to get the best of both worlds:
Tuning specific engines
Remember in the first post how we saw that model specifications in tidymodels define:
-
what type of model to use e.g. 'linear reg'
-
the 'mode' e.g. regression/classification
-
the 'engine' i.e. which modelling package we want to use e.g. glmnet.
We can see which hyperparameters are available for each model specification by calling the help function ? on our model spec. This shows us the hyperparameters that are common across all the engines for the model type:
But there are some engines that come with extra hyperparameters or options that are specific to themselves. To specify these, rather than set our engine as part of the model spec, we can leave that section blank and then set it more explicitly using the set_engine() function. This functions then allows us to pass engine specific arguments into our model spec. Let's see an example where we swap out the default 'nnet' engine for our mlp with 'brulee' which has some extra parameters we can then include for tuning as part of our specification:
Tuning hyperparameters
Now we've created our model specifications we can train our model and and tune our hyperparameters. Tidymodels has a few different options for creating hyperparameter combinations that we'll go through. We'll also see later some more advanced methods that conduct iterative searches of the hyperparameter space to try and find the best combination of parameters.
To tune hyperparameters we take our tunable model spec and train it with the tune_grid() function which tells tidymodels that we want to do some hyperparameter tuning. This replaces the fit_resamples() we were using in the previous post but tune_grid() still allows us to use our resampling scheme so we can get robust estimates of the model performance. Let's have a look at the simplest way to get tidymodels to tune our hyperparameters for us:
From the output we can see that we've got the results for 10 different models, each with a different combination of 'penalty' and 'metric' (our hyperparameters) tried. We can see that the first two models didn't perform very well but most of the others were pretty stable around 0.122 MAE. It's worth noting here that these error rates are calculated from our resampling scheme which was 10 folds x 5 repeats. As this is repeated for each of the 10 hyperparameter combinations we ended up training 10 folds x 5 repeats x 10 hyperparameter combinations = 500 models in total!
We got 10 different combinations of hyperparameters as, by default, when we tell tidymodels to tune hyperparameters but don't pass it any other options as per the documentation: "a semi-random grid (via dials::grid_latin_hypercube()) is created with 10 candidate parameter combinations". We'll learn more about Latin hypercubes later.
If we want to try more of fewer combinations of hyperparameters we can do this using the 'grid=' option. This is same option we'll use later to pass our own grids of hyperparameters that we'll create separately to the model training process.
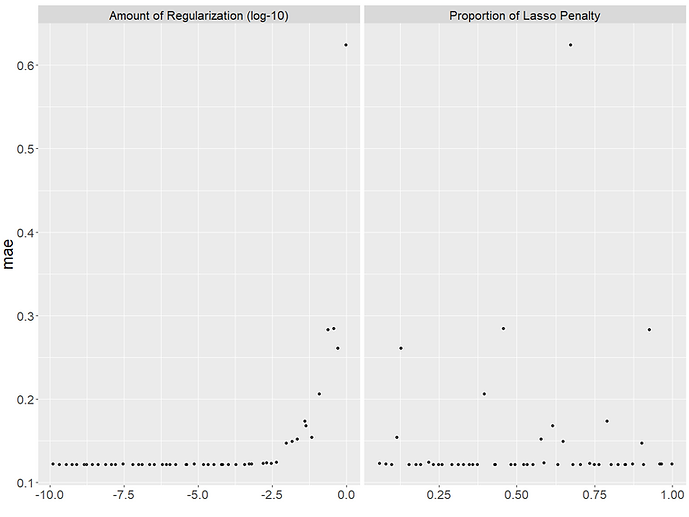
The plot shows us the performance of each of our 50 models for each hyperparameter combination. It can be a useful way to understand which values led to better model performances. For our model, it looks like smaller values of penalty i.e. 'regularisation' worked better but that the mixture i.e. 'proportion of lasso penalty' didn't matter as much as we got good models at higher and lower values of it.
We'll see two techniques later on that make use of this idea of using past hyperparameter results to guide their search of the hyperparameter space to try and find the best combination. We'll also see a way to avoid spending too much training models with obviously bad hyperparameters.
Manual, Regular and Random Tuning Grids
Tidymodels provides lots of ways to create grids of hyperparameters via the dials package. We'll look at how we can create them manually as well as grid_regular() and grid_random() first before looking at some more advanced methods.
Tidy models accepts hyperparameter grids as a tibble with a column name for each hyperparameter. For our glmnet specification the two hyperparameters are 'penalty' and 'mixture' so we can easily create our manually specified grid using the crossing() function:
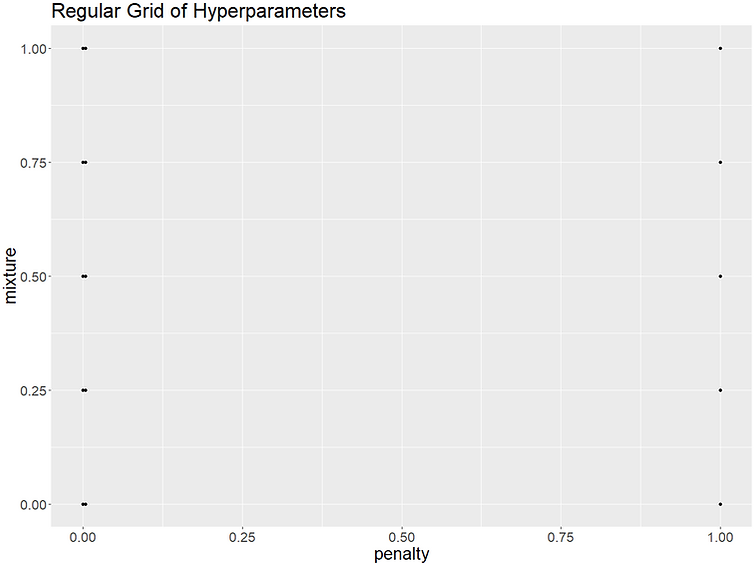
For both regular and random grids we specify which hyperparameters we want values for and then a value to determine how many different combinations to create. For grid_regular() we do this via the 'levels=' options whereas for grid_random() we use 'size=':
The 'levels=' of grid_regular() sets the number of values per parameter which are then cross joined to make one big grid that will test every value of a parameter in combination with every other value of all the other parameters. So our 5 levels x 2 hyperparameters makes for 5^2 = 25 hyperparameter combinations in our grid.
For our grid_random() on the other hand 'size=' tells tidymodels precisely how many hyperparameter combinations to create. These are randomly sampled from the hyperparameter space so there's a chance we'll explore a wider search area but we don't test every possible combination from within our space like grid_regular does.
As well as manually specify which hyperparameters we want to create values for, we can have tidymodels extract the hyperparameters from our model spec for us. This can be handy when our model spec (like we saw for our neural network) can have a lot of parameters to tune. We can do this using the extract_parameter_set_dials() function which uses our workflow to get the list of available hyperparameters for our model. We can also use the extract_parameter_dials() function to see what possible values each of our hyperparameters can take:
We can see that there are a wide range range of values available for both hyperparameters. The worry with grid_regular() is that by generating a small value of each parameter and cross-joining them, we can end up with very large grids that are slow to search but also might not explore the space fully. The worry with random grids is that as we sample randomly, we can have overlapping values of parameters so we effectively waste one of our training iterations by training overly similar models. We can plot the values created by each of the approaches to see how they vary and also understand some of their limitations. To make the process a bit more automated we can extract the parameters from our workflow as part of our grid creation:

Space-filling parameter grids
Tidymodels has two space-filling parameter grids available for us to use which "construct parameter grids that try to cover the parameter space such that any portion of the space has an observed combination that is not too far from it". These are the grid_latin_hypercube() and grid_max_entropy(). In theory, both of these should give us hyperparameter combinations that make fuller use of the space available and increase our chances of finding the best combination. Let's try plotting the parameters generated by both grid types to see how they compare:
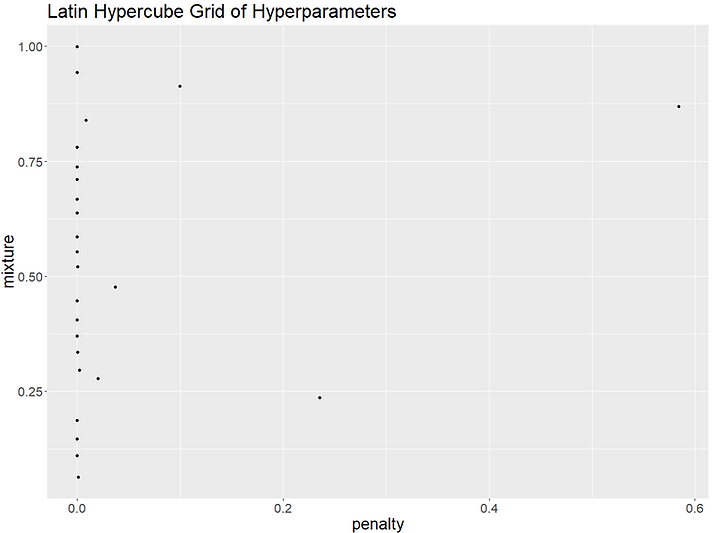
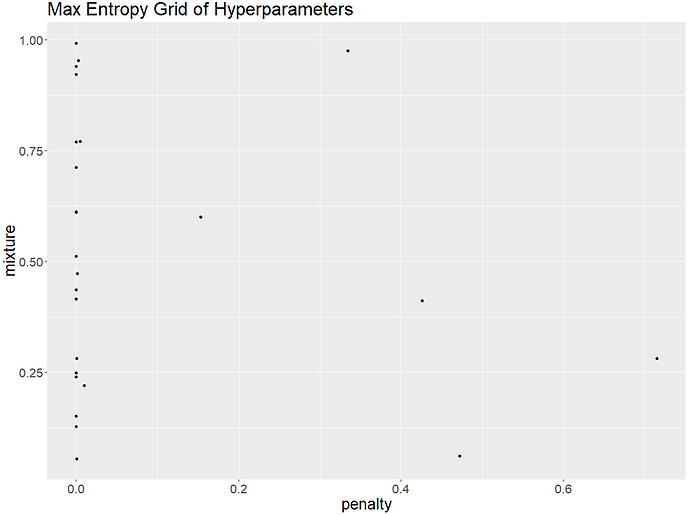
It looks like the regular grid is unusual in picking a penalty value of 1 as most of the other grids only have a few higher penalty values. We can compare the performance of each of our grids to see which generated the best hyperparameter set. We'll train all the models as specified by our different grids, keep the best performing model for each grid type and then compare to see which approach gave us the best overall hyperparameter values:
So it looks like on this occasion the random grid, closely followed by the Latin grid, gave us the best hyperparameter combination. We can see though that the performance of the top model from each type is very similar in performance which should reassure us that tidymodels does a good job of picking sensible values whichever approach we chose to take.
Finalising unknown hyperparameter values
We saw earlier when extracting the different values for 'penalty' and 'mixture' from our workflow that tidymodels populates the range of values each could take for us. This range is then used to generate the different hyperparameter values that populate our grid. Sometimes though, the range for the hyperparameter can't be known in advance and so we need to 'finalize' it before we can ask tidymodels to generate values of it for us.
For example, a lot of ensemble methods use a subsample of the available columns to train each base model and how many columns they can sample is a hyperparameter that we can tune. To create sensible values for our grid, tidymodels needs to know how many columns are in our training data. We have two options for this. The first is that we just let tidymodels generate the grid when we come to train our workflow. As all the pre-processing steps are applied when we train the model, tidymodels runs an extra step to finalise the values that each of the hyperparameters can take before it creates its grid:
If we now ask tidymodels to train our model for us it will do so and print a note to the log: "i Creating pre-processing data to finalize unknown parameter: mtry". This is particularly helpful for a value like mtry as it's the number of randomly sampled columns to be used during the model training which in turn also depends on our recipe and pre-processing steps. For example, our initial data set might have 10 columns but some of these might be categorical. If we choose to create lots of dummy variables we could quickly end up with a data set with 100+ columns which would greatly influence the values of mtry we'd want to try in our model.
If we want to create our grid of hyperparameters before our training process then we need to manually finalise the values using the finalize() function. We need to do this on our baked/pre-processed data so that any transformations such as dropping near zero variance columns, creating dummy indicators, etc. are taken into account. First let's extract the parameters from our workflow as we'll get a note about which parameters need finalising:
We can see we get a note that 'mtry' needs finalising and a handy suggestion of which functions to look at to achieve this. Let's now use the update() function with finalise() to update our parameter set with the correct value for mtry derived from our preprocessed training data. As we're only using the data to get the correct number of columns we don't need to worry about pre-processing our recipe on a separate sample of anything like that:
We can now pass our finalised/updated parameter set to our chosen grid function to create our final hyperparameter grid:
One thing worth mentioning is that for something like mtry which is the number of columns to randomly sample I've occasionally had issues where the near-zero variance pre-processing option removes some extra columns when run during resampling compared to when baked on train as a whole. This doesn't cause any errors but you'll get a message from tidymodels along the lines of "mtry=25 but only 24 features found".
As well as creating grids of hyperparameters and then passing them to our model to be tuned, we can also pass the updated parameters directly to the model training process. We do this by using the 'params_info=' option inside our tune() object. This can be handy for some of the more advanced hyperparameter tuning functions we'll see later where we might not want to pass a ready-made grid of values. The below example uses the tune_bayes() function which we'll see more of later:
Faster Hyperparameter Tuning with Racing Methods
The main downside of hyperparameter tuning is that it can take a long time. To find the best combination we have to build lots of models and assess their performance in a robust way which usually means lots of resampling. We saw earlier as well that some combinations of hyperparameters resulted in some pretty poor models. To help speed things up, tidymodels has the tune_race_anova() function. You can see a video of Max explaining how it works in tidymodels here.
The idea is that we can save time by weeding out any obviously bad hyperparameter combinations early on in the resampling process rather than waiting until the end. In our case, we’re using 10 folds repeated 5 times to assess our models, so that’s 50 resamples. If we can see that a certain combination of hyperparameters results in a really bad model, compared to its peers, after say 10 resamples, it’s probably safe to assume it’s not going to magically improve and beat them all after the other 40 resamples.
How it works in practice is that after a set number of resampling iterations tidymodels conducts an anova test and any model that is significantly worse than the current best is discarded. The remaining models then get tested again after more resampling with the significantly worse performers removed again. This carries on until either there is only one, significantly better hyperparameter combination left or until all the resampling has been completed and the best model is selected as normal.
The speed advantage is that, rather than try every combination of hyperparameters on every single resample, which can take a long time, we try every combination on only a few resamples and then only persist with the best ones. There is a time cost involved in calculating the anova test so it tends to work best with models that are slow to train. Let’s compare the time taken to run our xgb_workflow with a grid of 25 hyperparameters with and without using the racing method. The only code difference we need is that whereas before we used tune_grid() to train our model now we use tune_race_anova():
We can see that for both approaches we ended up with the same final set of hyperparameters but that the tune race was roughly twice as fast! Interestingly the error mean is slightly different between the runs which might be down to how many resamples the tune_race_anova() used to calculate it. We can plot the results of the race using plot_race() to see how many of the 100 hyperparameter combinations dropped out at each point during the resampling process:
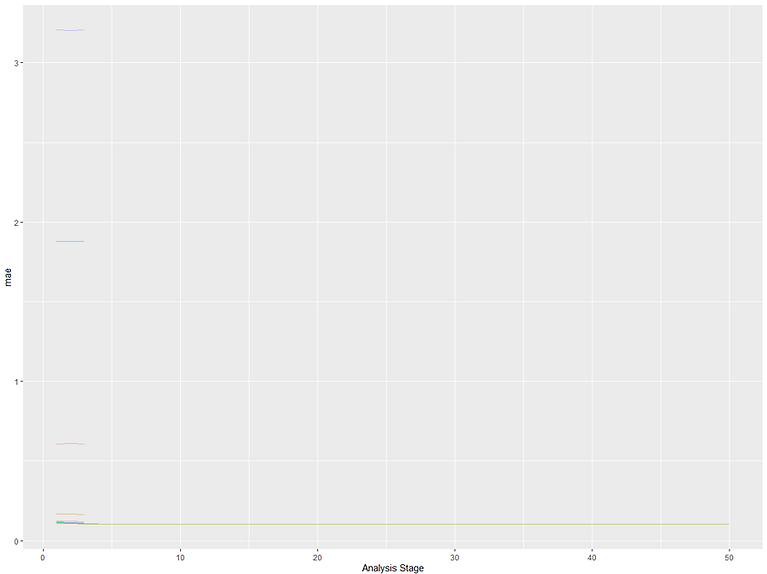
It looks like most hyperparameter combinations could be eliminated fairly early on which is what led to the time saving. There's a blue/turquoise line at the bottom that managed to make it a bit further but then got eliminated too, leaving our best combination as the only remaining candidate.
Bayesian optimisation of model parameters
So far we've been tuning using fixed grids of values to tune our model i.e. we generate our grid and then train using values from it. Now we're going to look at two approaches to hyperparameter tuning that take our initial grid and then use it to generate and explore new values of hyperparameters to try and find even better combinations. These are iterative search methods and it's well worth reading the chapter in the tidymodels book on the subject.
The first technique we'll look at is Bayesian optimisation. This takes the previous models' performances for each of the existing hyperparameter combinations and uses them to create a model. The model generates new values of hyperparameters and works out what their expected performance will be which are then tested by training the original model with them. This can continue for a set number of iterations or can finish early if we stop seeing an improvement. You can see Max giving a quick overview of it here.
To implement Bayesian search in tidymodels we use the tune_bayes() function. A lot of the options are very similar to our previous tuning approaches except this time we have an 'iter=' option that tells tidymodels for how many iterations to run the tuning. There's also the 'initial=' option which is where we pass the initial grid of hyperparameters to kick off the process with.
What's cool about tune_bayes() is this initial grid can either be an integer which tells tidymodels to create it's own initial grid of that size to learn from or it can be the results of a previous tuning grid run. This means we could say run a tune_grid() or tune_race_anova() to tune an initial grid and then run tune_bayes() subsequently to try and improve our model even more! We'll try both approaches. I'll also add in a 'control =' that tells tune_bayes() to stop early if it doesn't see an improvement after a certain number of iterations.
The 'verbose=TRUE' in the control gives us the long and detailed print out (I've truncated it) of what's happening at each iteration. We can extract the top model like we normally would and also plot the results of each iteration to see how it performed. This can be useful as we can see if performance was converging on a likely optimal or if it looks like it was still improving up to the final iteration, we might choose to run it again but for more iterations.
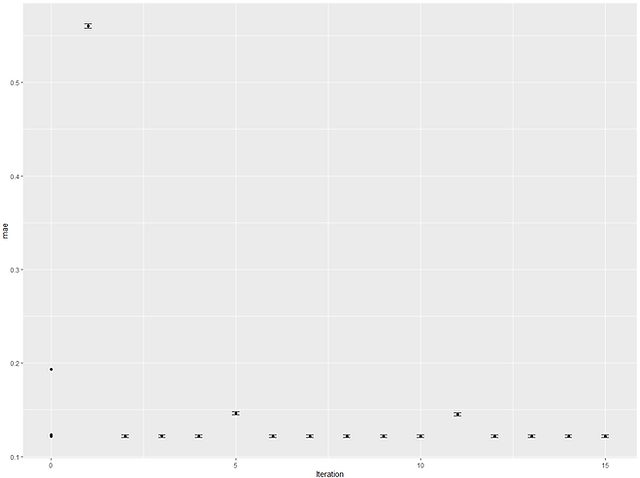
So it looks like the best model was actually found at iteration 6. Looking at the plot, the scores look like they'd plateaued but this might just be down to the scaling from the one really bad iteration. As mentioned, we can also run tune_bayes() using the output of a previous tuning grid. Let's create a tune_grid object that is a Latin hypercube with 50 hyperparameter combinations. We can then pass this to our tune_bayes() to see if we can improve upon it:
So it looks like on this occasion there was no improvement on our grid and the tune_bayes() process ended early after it couldn't find any improvement after 10 iterations.
Hyperparameter optimisation using simulated annealing
The tune_sim_anneal() function actually comes from the finetune package which is where tune_race_anova() also comes from. It draws inspiration from how when heated metals cool their particles can randomly rearrange themselves which can lead to stronger bonds being formed.There's a great summary of it in the tidymodels book in the chapter on iterative search. There's also a video of Max explaining how it work here.
'It is a global search method that can effectively navigate many different types of search landscapes, including discontinuous functions. Unlike most gradient-based optimization routines, simulated annealing can reassess previous solutions.'
- Tidy Modeling with R: Chapter 14
How this works with hyperparameter tuning is that an initial set of hyperparameters are created and assessed and then each parameter has a small change applied to it at random. The new values are then assessed and if they lead to an improvement they're used in the next iteration of having the small changes applied.
If the performance gets worse they still might get used as the hope is that even if they're not better straight away, they still might eventually lead to an improvement vs the current best eventually. In this way, simulated annealing is a 'non-greedy' method as it allows the optimisation to follow a path that isn't always the next best available step in the hope that 'taking the scenic route' eventually lands it on a better overall solution. The trick is to not follow the worse path all the way to a really bad solution so there are steps that can be added such as restarting at the last best solution after a certain number of iterations with no improvement.
The implementation of it in tidymodels is very similar codewise to how we were running tune_bayes(). We can either run tune_sim_anneal() with an initial set of hyperparameters created as part of the process or we can pass it the results of a previous tuning grid. There's also the control_sim_anneal() option which controls things like after how many iterations of no improvement to restart the process at the last best combination or how much of a small change can be made to the hyperparameters at each iteration:

In our example it looks like the best combination was found at iteration 3 but we could easily let it run for lots of iterations if we wanted to. Let's try running it with an already tuned grid and we'll use the control option to restart it a bit sooner if it doesn't find an improvement:
It looks like, as with the Bayes optimisation, once again our process couldn't improve upon our initial grid of hyperparameters. This might be because we're not running it for very many iterations but could also be a sign that tidymodels does a good job picking good original hyperparameters for us when we create our initial grids.
Tuning lots of models in a workflowset
So far we've just been training one model at a time and reusing the same recipe. We saw in the previous post how we can combine multiple models and recipes into a single workflowset. We can follow the exact same approach for tuning our hyperparameters. First we'll create each of our modelling specifications detailing which hyperparameters we want to tune. For the tree based ensemble models we'll just hardcode 'trees = 1,000' but for all other models and parameters we'll let tidymodels tune them for us.
As well as our model specifications we also need to create some recipes. I'll keep them fairly simple but to show off the value of using a workflowset I'll create 3 versions each with progressively more transformations to suit the needs of the different model types. Tidymodels has a handy reference guide for which models like which transformations here.
For creating our workflowset I'm taking advantage of the fact you can bind different workflowsets together. This allows me to cross join the model-recipe that I want without having to specify them all manually or remove the model-recipe combinations that I wouldn't want running. You can find a more detailed guide to creating workflowsets in the first post. As we'll be training and tuning 11 models I also create a quicker 5-fold cross-validation scheme to use.
Now we've created our workflowset we can run it! This will take quite a while to run so if your machine has been struggling I'd suggest using a smaller grid and maybe commenting out some of the longer-to-train models which you can see in the print out below.
We can see how each model performed exactly the same as before by calling rank_results() function. This will return each model-hyperparameter combination ranked from best to worst:
So it looks like our top 10 models (out of 265) are all different versions of the cubist model. This is helpful to know but perhaps we'd like to know how the best hyperparameter combination per model performed so we can compare them? To do this we still use rank_results() and simply add in the option 'select_best=T':
That's a bit easier to read. We can see that the cubist model did indeed perform the best with a MAE of 0.08. The next best models are the neural network, xgboost and SVM-poly all around 0.09. We can use autoplot with the 'select_best=T' option to plot the results and compare performance too:

If we want to fit our final model so we can predict on the Test set, first we need to extract the workflow of the best performing model and then extract the best hyperparameter combination from that workflow. We can then use those hyperparameters to update our workflow which allows us to fit our final model on the Train data and predict on the Test set. It's a little bit of an involved process but we can work through it a step at a time. Let's start by getting the workflow ID of the best model by ranking the models again and picking the top ranked model:
Now we have the workflow ID of the best model we can move on to getting the hyperparameter combination that gave us the best model. We can do this using the extract_workflow_set_result() function combined with our nearly saved best workflow ID object:
We can now use these hyperparameters to update our workflow before we fit the final model. Remember that when we created our model specifications we left most of the hyperparameters as '=tune()'? Essentially what we're doing now is telling tidymodels to go back to our workflow and where previously we had those '=tune()' placeholders, to overwrite them with the actual hyperparameter values that we've derived from the best model in our workflowset.
We do this by extracting the workflow for our best model (which will include the '=tune()' model spec and our recipe) and then we pass the actual hyperparameters from the best model to the finalize_workflow() function to update the spec with the correct hyperparameters. We then can fit the model:
After fitting the model and predicting on the Test set we can calculate MAE on the Test set to see how it compares to our resampling estimates. We can also plot the actuals vs our predictions:
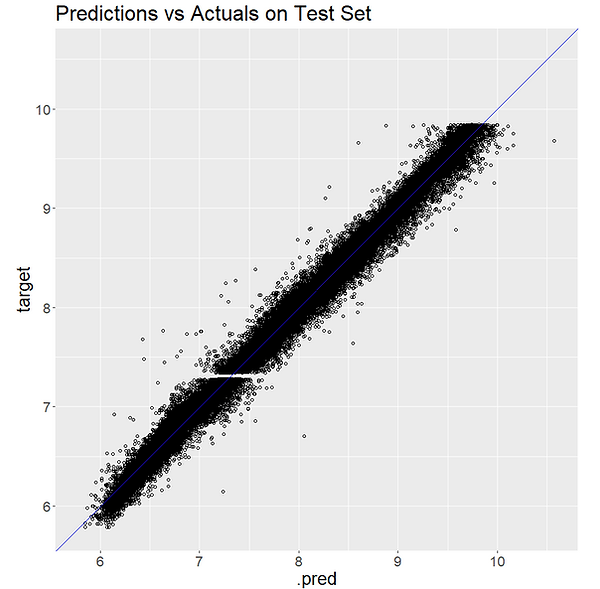
A score of 0.078 MAE on the Test set compares well with our estimate 0.08 MAE from the resampling. The plot also shows that our model seems to be performing well. Congratulations!
Model Stacking
We've been looking at how to tune the hyperparameters of our models to increase their performance. One last way of trying to squeeze out even more performance from our models is to try combining them or stacking them into a 'super learner'. To do this in tidymodels we can use the stacks package.
'Model stacking is an ensembling method that takes the outputs of many models and combines them to generate a new model - referred to as an ensemble in this package - that generates predictions informed by each of its members.' - stacks package
Essentially with model stacking we build an extra model that takes as its inputs the predictions of other models. The idea is that, similar to other ensemble methods, by combining multiple models into one, we can get something that is greater than the sum of its parts. To do this in tidymodels we need to save the resampled predictions from our models as they train so these can be inputs to our stacked model. We can add in a 'control=' option to our workflow to tell tidymodels to do this. Let's re-run our hyperparameter tuning workflowset from before but this time only keep the top 4 models and tell it to save the predictions as it trains:
We can see the results from our model tuning and again the cubist model looks to have created the best model. Although we've selected the best model per model type we've actually got 200 models (4 types of model x 50 hyperparameter combinations) behind the scenes which we can use with our stacks object.
We can incorporate our candidate models to incorporate into our 'super learner' we can create our stack model object using the stacks() function and then add our candidate models to it using the add_candidates() function:
We can see from the print out that we've got 199 models as one had to be removed as it was identical to another model already included. Now we've got added our candidate models to our stacks object we can use the blend_predictions() function to train our stacked model.
It does this by fitting a lasso model with different values of penalty/lambda and optimises it by picking the value that gives the best performance estimate on the resamples. As it is a lasso model it performs feature selection by setting the coefficient of any redundant columns to 0. This feature selection essentially removes any candidates models that aren't needed in the stack and only those with a coefficient>0 are kept:
We can see that out of 199 candidate models only 16 were kept. The 'weight' column shows us the relative weighting that each model's prediction has in the final stack. So we can see that the top two highest weighted models are both cubist, followed by 4 neural networks. We can use the autoplot() function to see how the stacked model performance varied for different values of lambda and also visualise the relative weights of each of the candidate models in the final stack:
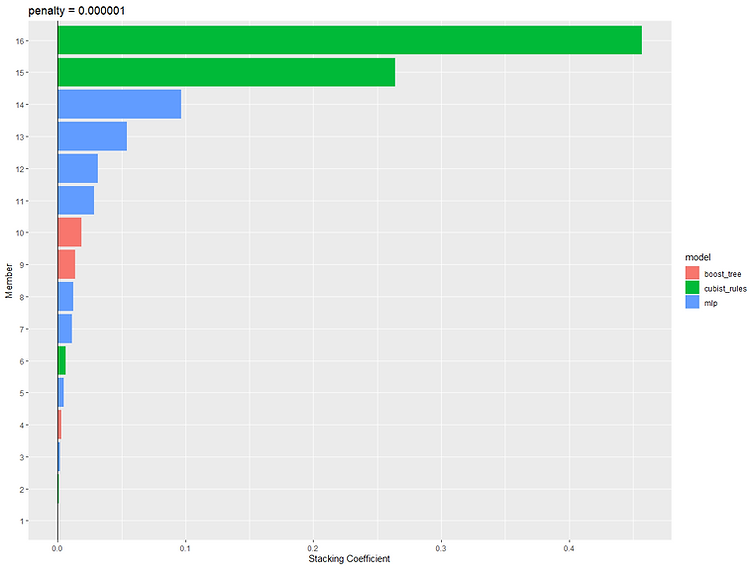
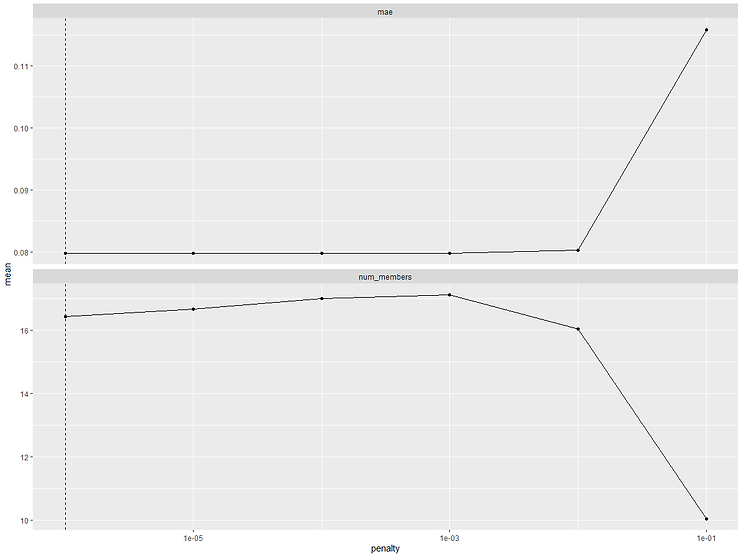
On the previous output there was a little note that said "Members have not yet been fitted with `fit_members()`". This is the last stage and is the same as fitting the final model on Train before we can score up Test. Let's do that now:
This will cause all of our candidate models and our stacked model to be trained one last time on all of the Train data so can take a while depending on how many and how complex your candidate models are. Once we've trained the models we can get predictions for the stacked model and each of its candidates and compare how they performed.
It looks like one of our cubist models actually slightly outperformed the stacked model although it's incredibly close. Even if the single cubist model had performed slightly worse, given it'd have much better speed, simplicity and interpretability as a single model solution I think we'd probably still have picked it over the stacked model anyway.
Congratulations!
That concludes this tutorial on hyperparameter tuning and model stacking using tidymodels. Well done for making it this far. Hopefully you feel confident now to try out some of the techniques outlined here in your own work. If you'd like to see how the equivalent can be done using the caret package you can find a tutorial on that here.


